Second Order Greeks in Options Trading
Intro to Second Order Greeks
As if the first order Greeks in options trading weren’t enough to understand, there are other factors that influence options pricing which some traders are less aware of. These are called Second Order Greeks. They are simply derivatives of the main Greeks: Delta, Theta, Vega. While the main first order Greeks are measuring sensitivities that affect the price of an option, the second order Greeks are sensitivities affecting the first order Greeks. Meaning they still affect the actual price of an option but not directly. If you aren’t that advanced in options trading or don’t think that Greeks matter to your trading I would say it’s just really good to know how these impact the entire market as a whole especially when markets become very volatile like they have been in 2022. As a general rule, option Greeks matter a whole lot more when volatility increases and so it’s good to learn for the sake of market awareness.
The main second order Greeks I will touch on are Gamma, Vanna, Vomma, and Charm. I know I know, what did he say?! Most traders have heard of Gamma and its actually used so often some may think of it as a first order Greek but it is actually the most important of the second order Greeks. Many “expert’s” will mention Gamma without knowing much about what they are talking about. The term ‘gamma squeeze’ became almost cliche during the 2020-21 meme stock craze. Gamma is important to understand if you trade options but for most traders that trade risk defined spreads for example its not going to have a large impact on things unless you trade a lot of weekly options near expiration. I wrote a separate piece on Gamma if interested in a more detailed explanation but here I will focus on the basics of these Second Order Greeks.
Gamma
As mentioned already Gamma measures how the options delta will change for a given change in the options value. Say you are short a 30 delta option, the gamma of this position will be dependent on what expiration cycle you are trading. The closer to expiration you are the higher the gamma will be. Farther out expirations have a lower gamma and thus the term gamma risk becomes more clear. Shorter dated options have much higher gamma sensitivity. A weekly option with a 30 delta might have a gamma of 2 or 3 times as high as an option with 60 days till expiration. This means a one point move in the stock will impact the price of the 30 delta option much faster in the weekly option.
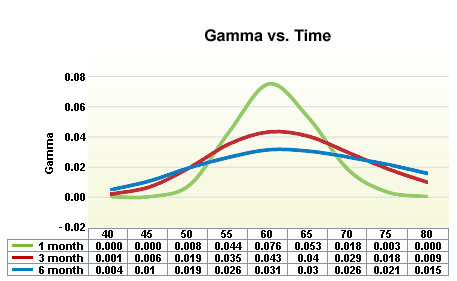
While weekly options might have a higher theta, you also get a higher gamma. This is the trade off if you are an options buyer looking for a fast move in the stock, gamma can be your friend while you have to combat the theta decay. As an options seller you would be selling gamma and buying theta. The risk to the options seller is a sharp move based on gamma, so thus it makes sense to sell options further out in time. You can see from the graph below showing Gamma vs Time that options with 1 month till expiration have a much steeper gamma curve. This simply means shorter dated options are much more sensitive to movements in the stock. So while the options with less than a month of time left have the highest theta, they often don’t give a lot of margin for error if you sell them and are wrong.
Vanna
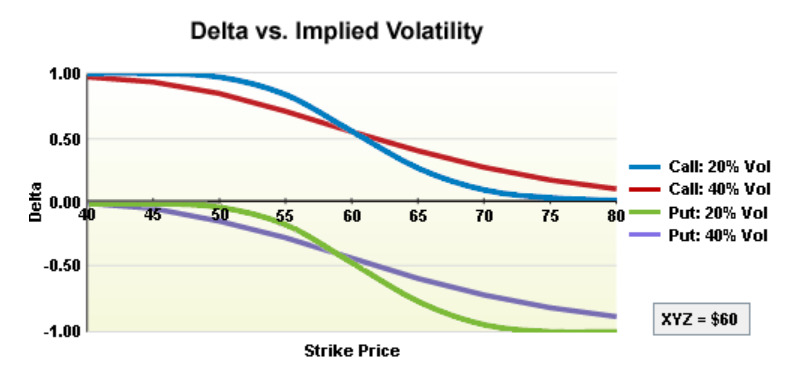
Vanna measures the change in delta for any change in implied volatility. Since the options that are most affected by implied volatility changes are out-of-the-money options, these are also the options that are most affected by Vanna. Sometimes during a wild spike in the VIX, markets see volatility skew rise and that is implied volatility rising in out-of-the-money options. When this happens the market is pricing in larger expected moves in the underlying market. This is when a 5 delta option can quickly turn into a 15 delta option and start to grow teeth. This is essentially Vanna exposure. As implied volatility rises sharply, the delta of the out-of-the-money options increase as well.
Part of what caused the GME short squeeze in early 2021 was a Vanna effect where implied volatility rose so high beyond what anyone could have imagined it forced the normally cheap 5 delta or less options to have much higher delta’s and basically strike prices 200% higher were being priced like they were much closer to the stock price than they actually were. This is what ignited the gamma squeezes in meme stocks as this explosion in implied volatility or vanna risk made it almost impossible for market makers to price what true risk was.
For the majority of traders Vanna really doesn’t matter, and is worth ignoring if all you trade are risk defined spreads or verticals. Vanna is much more important for market makers and big firms that need to quantify their risks on many levels as volatility changes in out-of-the-money options. Vanna also is more of a factor the closer to expiration an option gets. Often in volatile markets like we have currently, a market wide short squeeze can begin as expiring options start to decrease their delta’s closer to zero as IV falls so dealers will be forced to close any related hedges they have on. Multiply this by billions of dollars of hedging requirements changing and you can see these sort of rallies that start out of nowhere close to large options expiration dates.
Vomma
Vomma measures the rate of change of an option Vega for any given change in implied volatility. So this does not impact delta of an option much and thus is not really relevant for 99% of traders. Only the large professional options firms with constant Vega risk should be concerned with their Vomma exposure. For this reason it’s the least important Greek on this list but I still wanted to mention it to be aware. Similar to Vanna, the Vomma Greek is higher for out-of-the-money options.
Charm
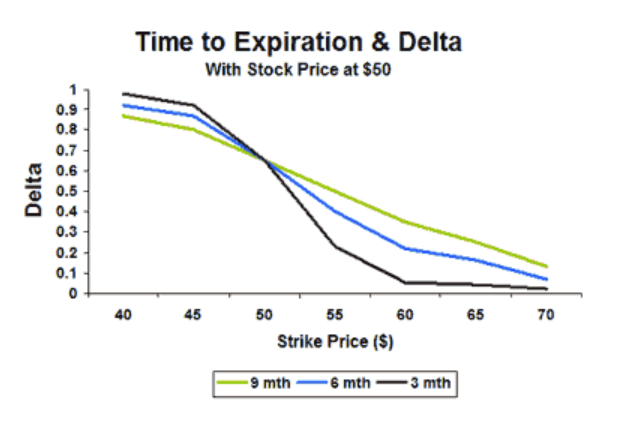
Charm is an interesting one as most have not heard much about it but it’s a constant in the world of options since it’s centered around theta decay or the passage of time. Charm measures the rate of change of delta for a given theta value. This is also called the “delta decay of an option”. Similar to Vanna it also affects out-of-the-money options more directly and shorter dated options the most. The closer to expiration an option gets the more it decays due to theta or time value passing.
As a retail trader as long as you understand the theta decay you are exposed to then that’s good enough but charm is more important for dealers or market makers that constantly need to hedge their delta exposure. Dealers are always trying to stay delta neutral so when an option position changes its delta based on time passing, or charm, then they will need to act to adjust their risk.
If you have ever watched an option you own decrease in value for each day that passes closer to expiration you might have also noticed the delta of that option decrease. That’s Charm. As an option’s life gets closer to expiring, the delta will decrease even if the price does not move.
Takeaways:
- Second Order Greeks are less important than first order Greeks but they are still important components that explain how options prices change over time.
- Gamma is the rate of change of delta for a given move in the options price.
- Vanna is the change in delta for any given change in implied volatility.
- Vomma is the rate of change in an options vega for a change in implied volatility.
- Charm is the rate of change in options delta for a given change in theta, or time passing.
