The last several posts discussing the Greeks went over Delta and Theta. For the third post in the series on Options Greeks we will cover Vega, which is related to how implied volatility factors into options pricing. Understanding how implied volatility affects options is really important especially if trading around key events such as earnings or in overall volatile markets. The delta and theta components are probably the two greeks that most traders understand first but Vega is sometimes overlooked unless you trade multi leg spreads or trades such as calendars or butterflies.

What is Vega?

Vega is the rate of change of an options value based on a 1% change in implied volatility. When IV moves due to supply and demand of people trading options it affects the price of the option based on that movement. The measure of this is called vega. In general when people buy options aggressively it drives up IV. When people sell options it pushes IV lower. You can think of Vega as the way to measure human behavior in the options market. When traders are fearful of downside they buy put options and this causes IV to spike. Often you will hear about the VIX index rising or falling due to fear or lack thereof. This VIX index simply measures the demand for options in the S&P 500 so it’s a good overall way to track market implied volatility. Historically, implied volatility tends to be mean-reverting even more so than stock prices so it’s common to see IV spike and then collapse back lower. 

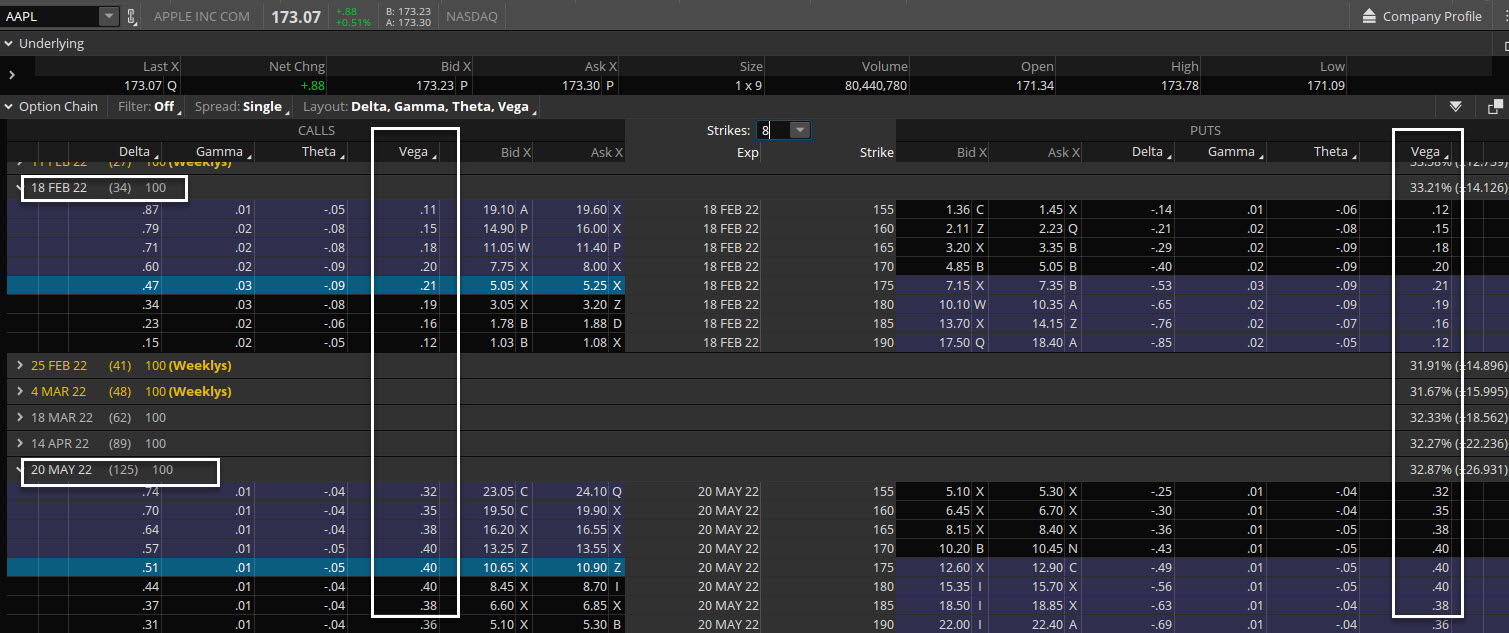
Vega is a positive number for option buyers and a negative number for option sellers. That means if you are a net buyer of options you are long vega and would prefer to see IV move higher. If selling options, you are generally doing that based on higher IV so you are short vega and want to see IV come back down to profit. For example, if I have an option like in the below image with an AAPL 175 call that is worth $5.00 and the vega is 21 this means that I stand to gain or lose $21 for every 1 point change in implied volatility in that option. If IV moves up 5 points that means the option would move roughly $100 (5 x 21) and you would profit as the long call buyer even if the stock price did not move much. That’s the cool part about implied volatility. However, this cuts both ways also as IV can often move lower, especially if it starts from a higher point. That’s why buying a simple long call or put is tough if not correct in direction right away. You are fighting against theta decay and oftentimes contracting implied volatility which can make options prices fall. The way to easily combat this risk is to use spreads as buying a call debit spread largely eliminates most if not all of the vega exposure of a naked long call since you are buying one option and selling another.

Vega Differences Based on Expiration Cycles

Vega is the opposite of theta in regard to expiration cycles. Theta decreases the further out in time you go since the closer expiration experiences higher rapid rates of theta decay. With vega, the near term expirations will show lower vega exposure than more longer term expirations. Since we know vega is the rate of change given a 1% change in IV, short term cycles that have fewer days to expiration tend to not have much effect on changes in vega. A big change in IV won’t really affect price that much, outside of maybe a near term catalyst like an earnings announcement in a stock. In general, an option with 100 days til expiration will have a higher vega and corresponding changes in IV will affect prices much more than an option expiring in less than 20 days. This is because there is still much more time for the stock to make a move so a higher IV will imply more potential movement. Looking at the AAPL option chain below you can see the clear difference in vega values for the February options with 34 days of life left versus the May options with 125 days till expiration. The Feb 175 calls have a vega of 21 while the May 175 calls are almost double the vega at a value of 40. This means that changes in implied volatility will be more pronounced in the longer dated options since the vega is higher. 

Selling Options when IV is Higher

This comes back to why option sellers are more interested in selling options when implied volatility has moved up higher compared to historical norms. If you are an options trader and you’ve ever tried to buy a long call or put when IV is elevated you likely were frustrated at some point if you were hit with a volatility collapse. The higher vega risk is what makes buying options hard when IV spikes higher. However, this makes premium selling strategies more favorable in times of higher volatility and premiums. Whether you sell a cash secured put or are using credit spreads to trade for a contraction in IV these are both great ways to use higher IV to your advantage and getting short vega. Also butterfly spreads are a smart way to use options to get short volatility in a faster moving market with juiced up premiums. If you are more advanced and have the experience and capital to sell strangles or straddles that is also another way to get short vega exposure in elevated implied volatility environments. In general the lower the implied volatility is compared to its 52 week range then the better it might be to be long vega option strategies such as long calls or calendar spreads. The higher the IV is compared to its recent range then the more advantageous that selling strategies can be since we know implied volatility tends to show mean reverting tendencies in the long run. Regardless of what your objectives are in an option trade it’s good to know where the IV might be headed next in order to put on the most effective option strategy and that makes vega an important options greek to be aware of when evaluating how sensitive a position might be to changes in IV.

Takeaways:

• Vega is the rate of change of an option’s extrinsic value, given a 1% change in the underlying stock’s implied volatility.
• Option buyers benefit from increasing IV, this makes the vega number positive. 
• Option sellers benefit from a decreasing IV, this makes the vega number negative. 
• Higher vega numbers exist in further out expirations with more time.
• IV has generally been mean reverting throughout history, thus IV spikes lead to collapses back down when fear subsides.